Секреты Большого Путешествия. Нахождение оптимального пути на этапе Лабиринт "Большое Путешествие - старшие"

 

Регламент соревнований “Большое Путешествие - старшие” определяет максимально возможное количество набранных баллов 400. И ключевым этапом этого вида соревнований является этап Лабиринта, так как Регламент начисляет 80 баллов только при обратном прохождении Лабиринта по кратчайшему пути, в противном случае 40. Поэтому перед каждым наставником стоит задача, какой алгоритм применять для определения кратчайшего пути. Эта же задача встала перед нами,  когда мы решили подготовить робота  для этого вида соревнований в нашем кружке спортивной робототехники с возможностью набора 400 баллов и прохождения всего маршрута менее 100 сек. У нас уже был опыт подготовки роботов для линейных лабиринтов с нахождением оптимального пути и опыт прохождения лабиринтов по правилу левой или правой руки, а также в настоящий момент мы готовим роботов типа микромышь для соревнований Лабиринт по регламенту КОР Белоруссия, где используем алгоритм “Flood fill”.

Исходя из этого опыта мы начали искать решение для нахождения кратчайшего пути при прохождении Лабиринта в обратном направлении. Первое что необходимо учесть в исходных данных - это то, что Лабиринт в Большом Путешествии имеет ряд ограничений, а именно:

1. Лабиринт имеет всегда размер 5х5 клеток.
2. Лабиринт всегда замкнутый.
3. Вход  и Выход в Лабиринте не меняются и остаются во всех комбинациях на определенных регламентом местах.
4. Количество клеток при прохождению по правилу “Левой или Правой руки”  всегда одинаково.

Анализ этих ограничений позволил сделать вывод, что существует ряд вариантов Лабиринтов, когда оптимальный путь можно найти при прохождении в обе стороны, но не для всех комбинаций Лабиринтов. И тогда стало понятно, что надо при прохождении Лабиринта по правилу Левой/Правой руки в направлении “Туда”  построить модель лабиринта и пути прохождения в памяти робота и при достижении черной поперечной линии следующего этапа Инверсная Линия при выходе из финишной ячейки оптимизировать эту модель для прохождения роботом пути “Обратно” по кратчайшему пути.

Сначала мы решили использовать алгоритм “Flood fill”, но этот вариант не позволяет использовать среду Scratch в виду ее ограничений  в которой наши школьники работают до 6-7 класса и он достаточно сложен в реализации, а ведь у нас простой закрытый Лабиринт. И после долгих поисков пришло решение - применить алгоритм изложенный в статье “Teaching a Robot to Solve a Line Maze” by Richard T Vannoy II April 2009"  /www.pololu.com/file//line-mazealgorithm.pdf для Лабиринта напечатанного на бумаге с некоторыми доработками для Лабиринта со стенками. Этот алгоритм существенно проще, подходит только для замкнутых Лабиринтов и не требует построения в памяти модели Лабиринта, а строит только модель пути и позволяет ее оптимизировать до нахождения кратчайшего пути. Но как использовать доработанный Алгоритм для Лабиринта со стенками?

Рассмотрим суть алгоритма. Она заключается в следующем:

1. Робот проходит лабиринт по правилу Левой или Правой руки.
2. В процессе прохождения он определяет узловые ячейки.
3. Находясь в узловой ячейке робот определяет тип дальнейшего движения, а именно: Поворот налево на 90 градусов (L) и прямо, Поворот направо на 90 градусов (R) и прямо, Движение прямо (S), Разворот на 180 градусов (B) и прямо.
4. Результат определения дальнейшего движения в  виде символов указанных в  п. 3 записывается в одномерный массив в виде последовательности символов.
5. Робот совершает выбранный тип движения, до определения следующей узловой ячейки, в которой п.п. 3-4 повторяются.
6. При достижении финишной ячейки ( определяется по черной поперечной полосе начала инверсного поля) робот строит в памяти кратчайший маршрут движения методом исключения дважды пройденных участков. В результате мы получим символьный массив соответствующий кратчайшему пути.
7. При прохождении лабиринта в обратном направлении робот также определяет узловые ячейки, но выполняет движение соответствующее символу в одномерном массиве по правилу: первая узловая ячейка - первый символ, вторая - второй и т. д.
8. В итоге робот проходит обратный маршрут кратчайшим путем.

Как определить узловую ячейку?

Для определения узловой ячейки робот должен иметь три дальномера, а именно: фронтальный, левый и правый для определения наличия стенок с трех сторон робота. Если робот в процессе движения прямо определил следующие варианты:

1. Присутствует стенка слева и отсутствуют стенки впереди и справа.
2. Присутствует стенка справа и отсутствуют стенки впереди и слева.
3. Присутствуют стенки впереди и слева и отсутствует стенка справа.
4. Присутствуют стенки впереди и справа и отсутствует стенка слева.
5. Отсутствуют стенки спереди, слева и справа.
6. Присутствуют стенки слева, справа и спереди.

то ячейка в которой находится робот является узловой. Неузловая ячейка всегда имеет две стенки слева и справа и не имеет стенки впереди.

Правило приведения одномерного массива

Для получения кратчайшего маршрута используется следующий алгоритм:

1. Находим в одномерном массиве символ “B” .
2. Находим рядом с ним два символа - один слева, другой справа.
3. Заменяем эти три символа  на один  следующим образом RBL - B, RBS - L, SBR - L, RBR - S  и т. д. Остальные комбинации замен можно подобрать в зависимости от лабиринта и движения по правилу Левой/Правой руки.
4. Проводим замены до тех пор пока в массиве не останется ни одного символа “B”.

Примеры определения кратчайшего пути

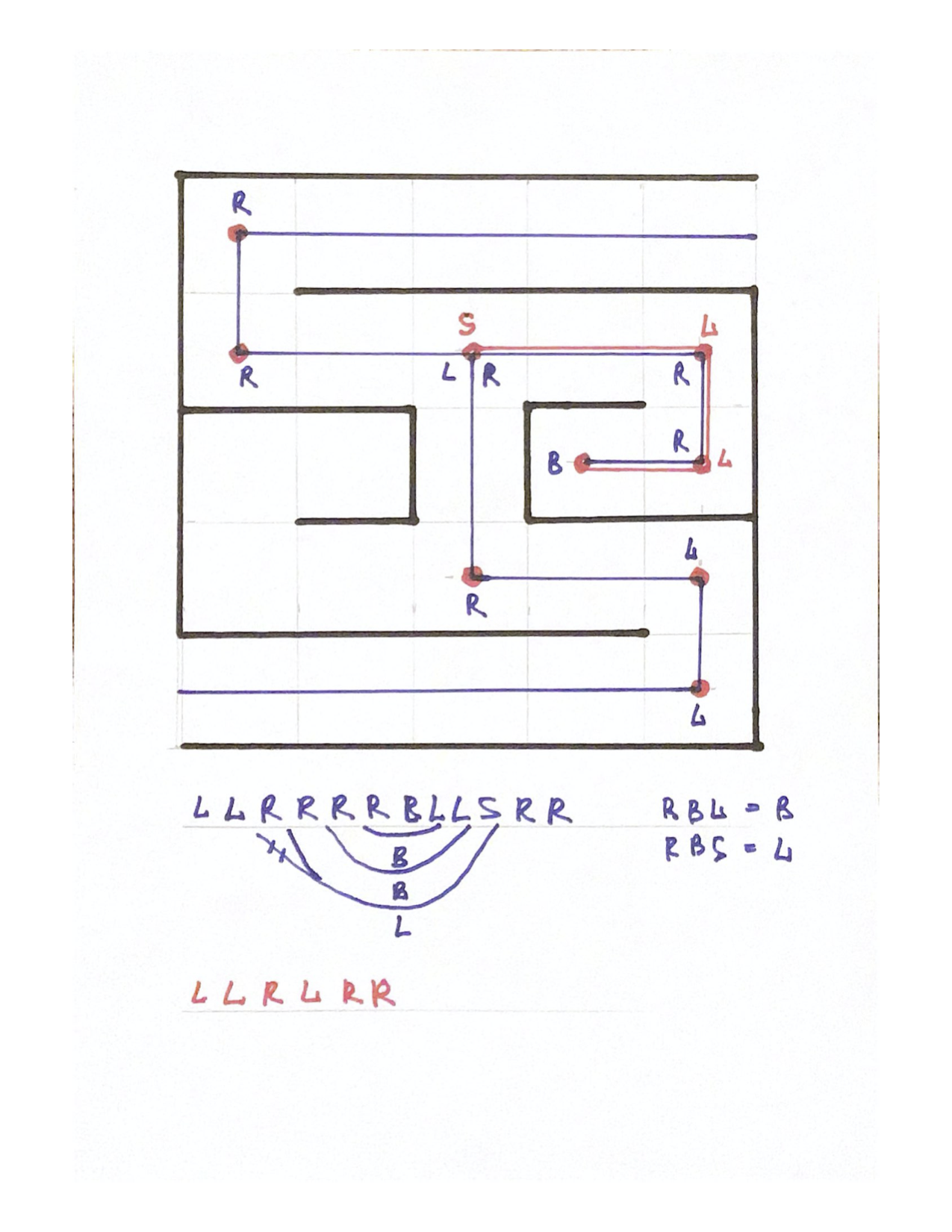
На обеих рисунках ниже красными точками отмечены узловые ячейки. Синим цветом проложен маршрут по правилу левой руки на первом рисунке и по правилу правой руки на втором рисунке. На обоих рисунках синим цветом показан одномерный массив с правилом приведения к кратчайшему маршруту. Красным цветом показан одномерный массив в результате приведения к кратчайшему пути. на первом рисунке красным цветом отмечен кратчайший маршрут, а на втором удаляемая ветвь.

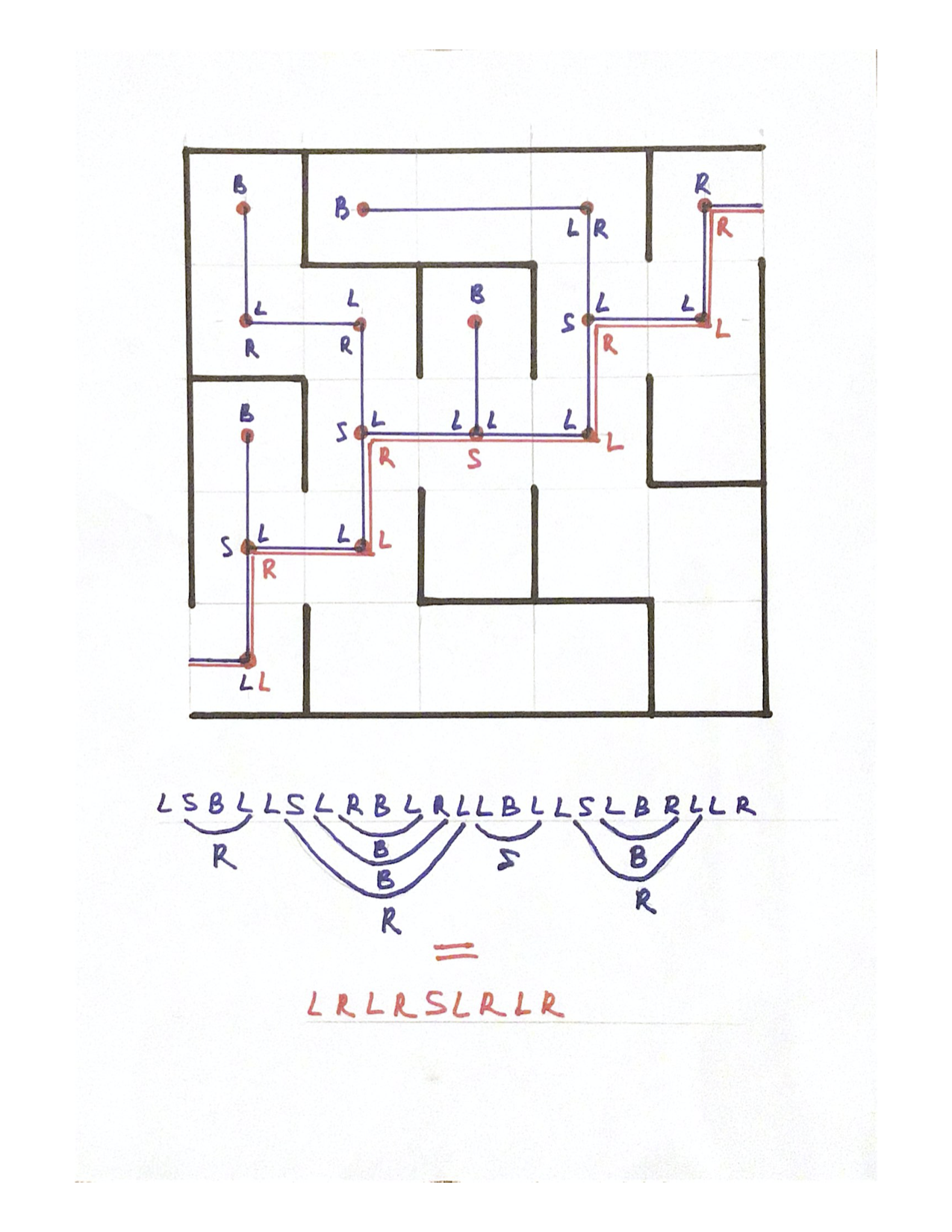
Пример прохождения роботом первого Лабиринта по кратчайшему пути в отладочном режиме приведен здесь https://disk.yandex.ru/i/7vdHsj6DNtTEPw.